Annotating Statistics onto Plots

Week 9

Author

Jessica Cooperstone

A cartoon that says 'I can't believe schools are still teaching kids about the null hypothesis - I remember reading a big study that conclusively disprovied it years ago — Figure from XKCD

Introduction

Now that we’ve spent some time going through how to make plots, today we will focus on how to annotate statistics that you’ve calculated to show statistical differences, embedded within your plot. I will go over a few different ways to do this.

The purpose of today’s session is more to give you practical experience with running and retrieving statistical analysis output, than teaching about the assumptions and background of the test itself. If you are looking for a good statistics class, I would recommend Dr. Kristin Mercer’s HCS 8887 Experimental Design.

Load libraries and data

Before we get started, let’s load our libraries.

We are going to use data that was collection about body characteristics of penguins on Palmer Station in Antarctica. This data is in a dataframe called penguins in the package palmerpenguins which you can download from CRAN.

a hexagon sticker in blue with a picture of a 3 cute cartoon penguins that says 'palmer penguins' — From Palmer Penguins

# install.packages(palmerpenguins)
library(tidyverse)
library(palmerpenguins) # for penguins data
library(rstatix) # for pipeable stats testing
library(agricolae) # for posthoc tests 
library(ggpubr) # extension for adding stats to plots
library(glue) # for easy pasting

knitr::kable(head(penguins)) # kable to make a pretty table

species	island	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g	sex	year
Adelie	Torgersen	39.1	18.7	181	3750	male	2007
Adelie	Torgersen	39.5	17.4	186	3800	female	2007
Adelie	Torgersen	40.3	18.0	195	3250	female	2007
Adelie	Torgersen	NA	NA	NA	NA	NA	2007
Adelie	Torgersen	36.7	19.3	193	3450	female	2007
Adelie	Torgersen	39.3	20.6	190	3650	male	2007

2 group comparisons (t-tests or similar)

Our question: Is there a significant difference in the body_weight_g of male and female penguins?

Before we run the statistics, let’s make a plot to see what this data looks like.

# what are the values for sex?
unique(penguins$sex)

[1] male   female <NA>  
Levels: female male

# plot
(penguins_by_sex <- penguins %>%
  drop_na(body_mass_g, sex) %>% # remove NAs for body_mass_g and sex
  ggplot(aes(x = sex, y = body_mass_g, color = sex)) + 
  geom_boxplot(outlier.shape = NA) + # remove outliers
  geom_jitter(height = 0, width = 0.3) + # jitter only in the x direction
  scale_x_discrete(labels = c("Female", "Male")) + # change x-axis labels
  theme_minimal() +
  theme(legend.position = "none") +
  labs(x = "Sex",
       y = "Body Mass (g)",
       title = "Body mass of penguins by sex",
       subtitle = "Collected from Palmer Station, Antarctica",
       caption = "Data accessed from the R package palmerpenguins"))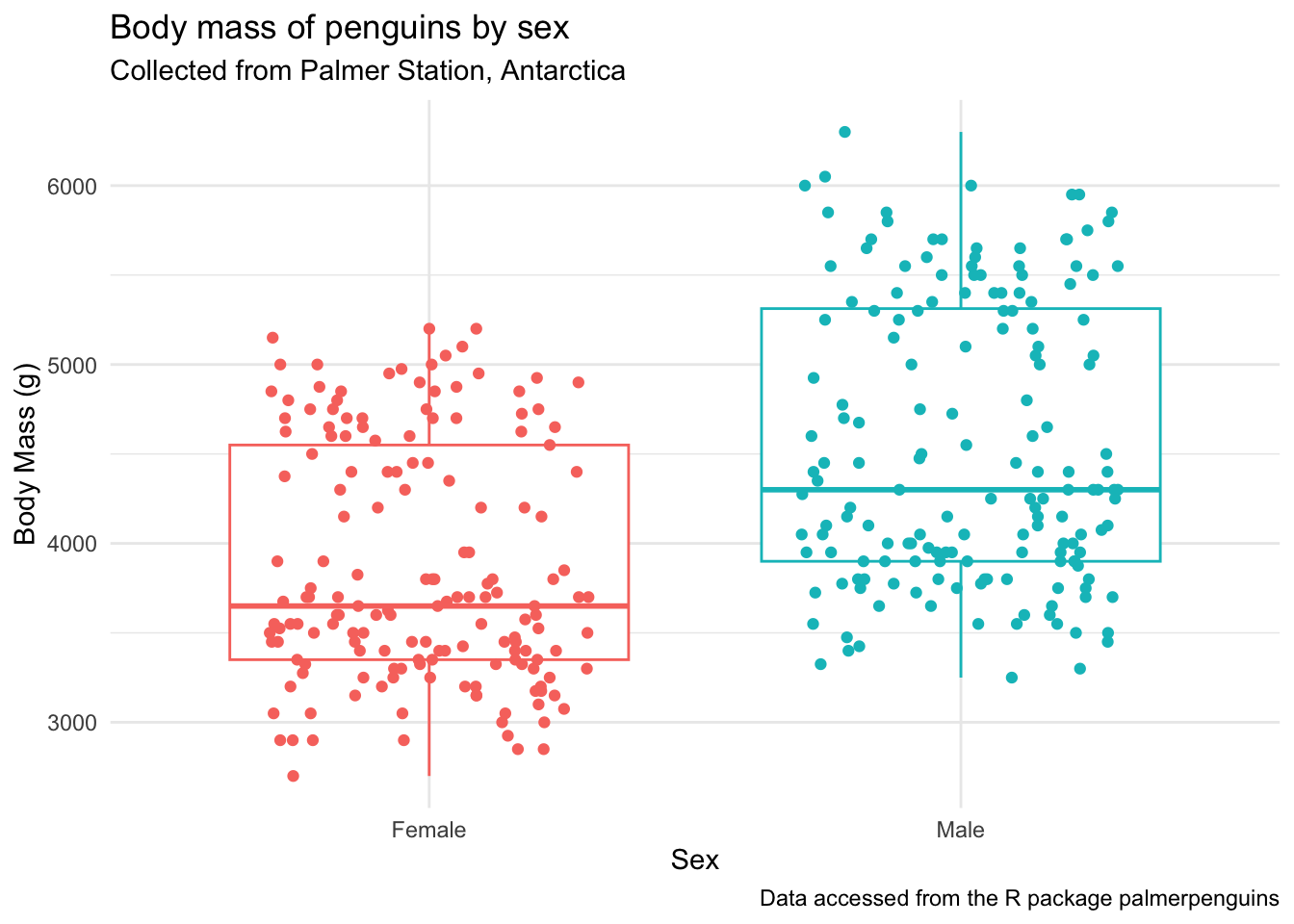

It looks like there is a difference here. Before adding the statistics to our plot, let’s:

test that our data is suitable for running the text we want
run the statistical test separately from the plot

Testing assumptions

Briefly, in order to use parametric procedures (like a t-test), we need to be sure our data meets the assumptions for 1) normality and 2) constant variance. This is just one way to do these tests, there are others that I am not going to go over.

An orange normal distribution and a blue bimodal distribution where the orange distribution tells the blue one it is not normal — Illustration by Allison Horst

Normality

We will test normality by the Shapiro-Wilk test using the function rstatix::shapiro_test(). This function is a pipe-friendly wrapper for the function shapiro.test(), which just means you can use it with pipes.

penguins %>%
  drop_na(body_mass_g, sex) %>% # remove NAs
  group_by(sex) %>% # test by sex
  shapiro_test(body_mass_g) # test for normality

# A tibble: 2 × 4
  sex    variable    statistic            p
  <fct>  <chr>           <dbl>        <dbl>
1 female body_mass_g     0.919 0.0000000616
2 male   body_mass_g     0.925 0.000000123

This data is not normal, which means we need to use non-parametric tests. Since we are not meeting the assumption for nornality, really you don’t need to test for constant variance, but I’ll show you how to do it anyway.

Constant variance

We can test for equal variance using Levene’s test, levene_test() which is part of the rstatix package. Again, this is a pipe-friendly wrapper for the function levene.test().

penguins %>%
  drop_na(body_mass_g, sex) %>% # remove NAs
  levene_test(body_mass_g ~ sex) # test for constant variance

# A tibble: 1 × 4
    df1   df2 statistic      p
  <int> <int>     <dbl>  <dbl>
1     1   331      6.06 0.0143

No constant variance. Double Non-parametric.

Can we visualize normality another way?

penguins %>%
  drop_na(body_mass_g, sex) %>%
  ggplot(aes(x = body_mass_g, y = sex, fill = sex)) +
  ggridges::geom_density_ridges(alpha = 0.7) + # density ridgeline plot
  scale_y_discrete(labels = c("Female", "Male")) +
  theme_classic() +  
  theme(legend.position = "none") +
  labs(x = "Body Mass (g)",
       y = "Sex",
       title = "Distribution of body weights for male and female penguins")

Picking joint bandwidth of 235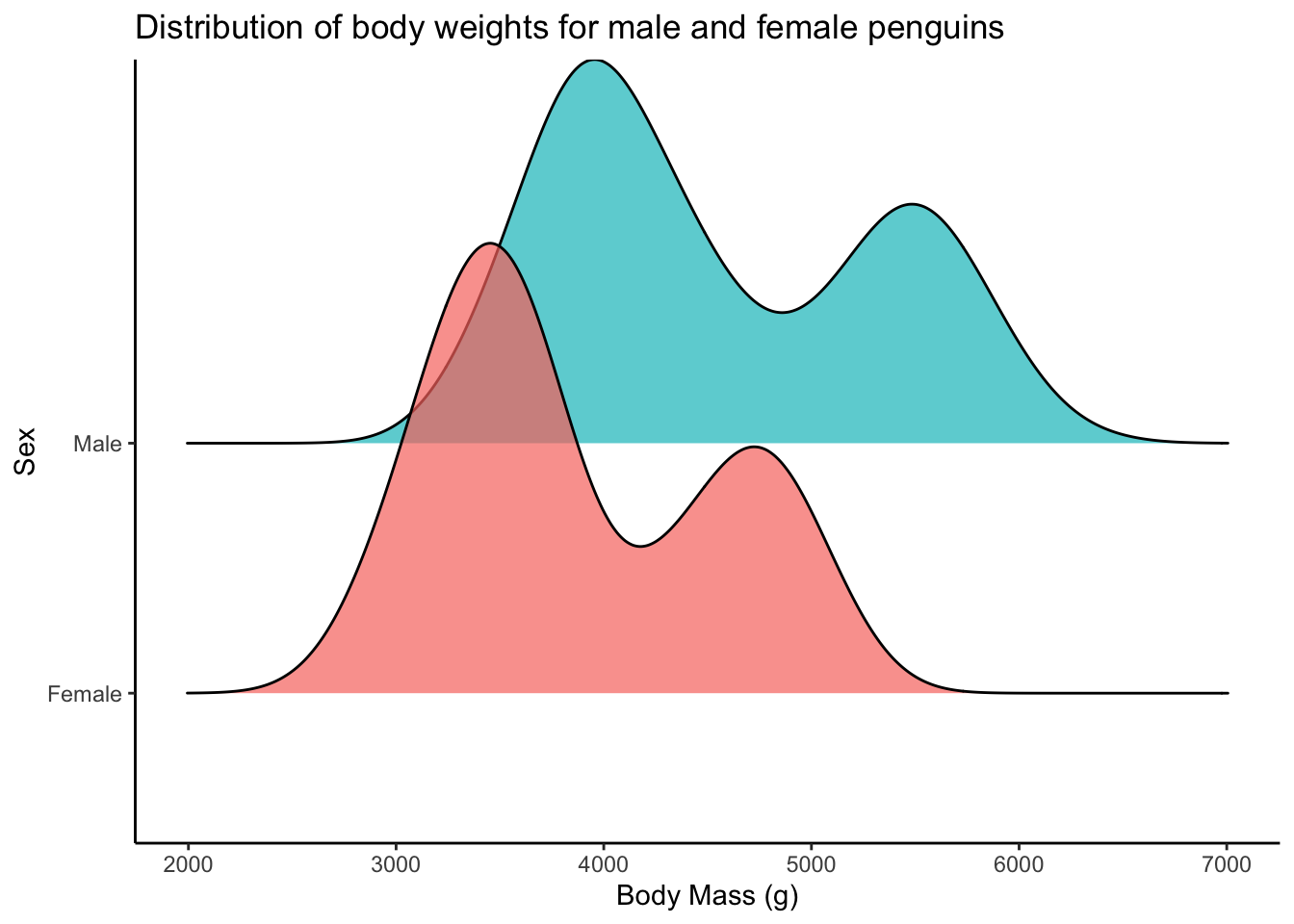

Some of these distribution are bimodal (i.e., not normal). This is likely because we have 3 different species of penguins here. You can see below that actually each species looks reasonably normal.

penguins %>%
  drop_na(body_mass_g, sex) %>%
  ggplot(aes(x = body_mass_g, fill = sex)) +
  geom_histogram() +
  facet_grid(cols = vars(species), rows = vars(sex)) + # 2 way facet
  theme_classic() +
  theme(legend.position = "none") +
  labs(x = "Body Mass (g)",
       y = "Count")

`stat_bin()` using `bins = 30`. Pick better value with `binw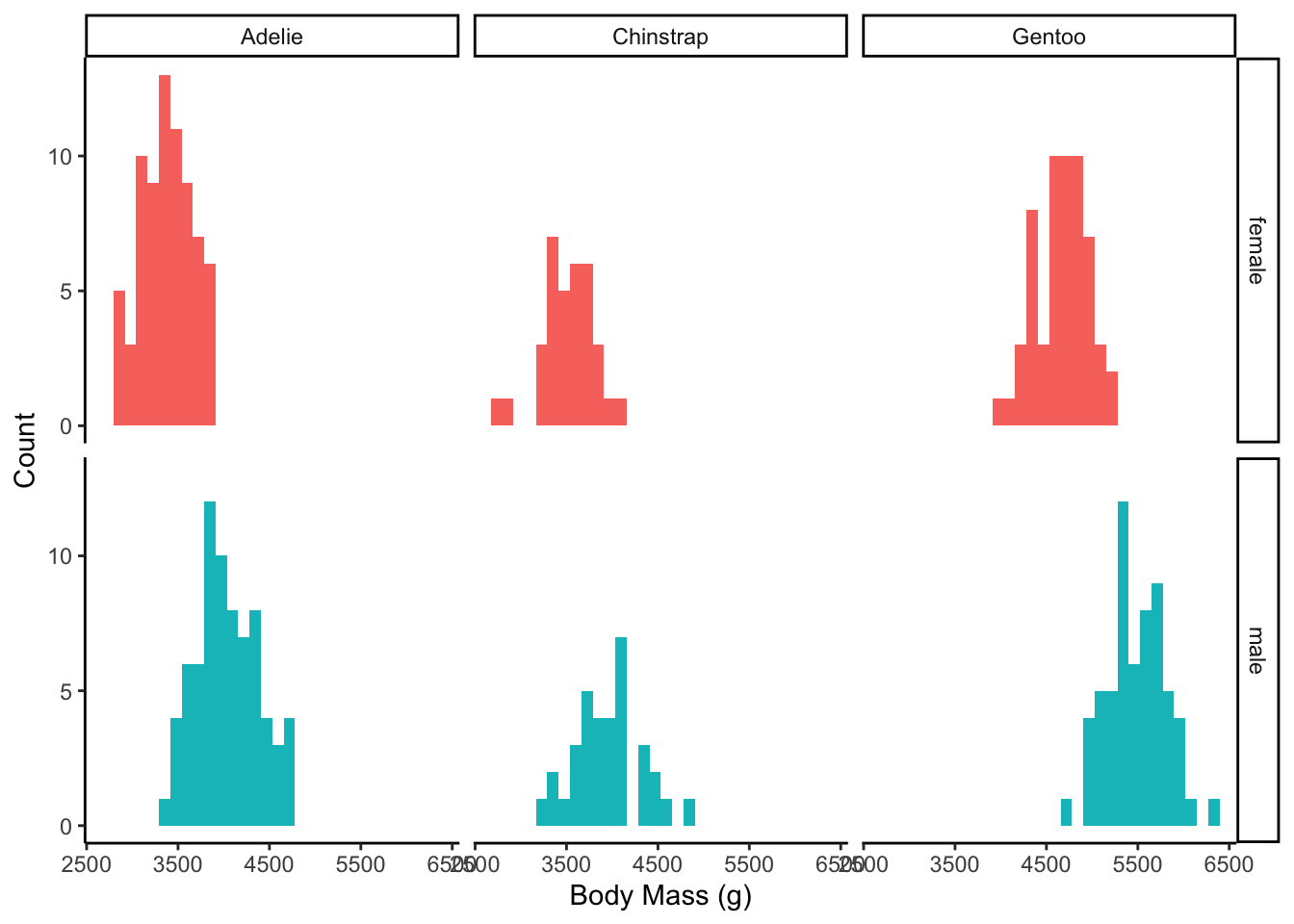idth`.

Non-parametric t-test

This means if we want to test for different means, we can use the Wilcoxon rank sun test, or Mann Whitney test. If your data was normal, you could just change wilcox_test() to t_test() and the rest would be the same.

penguins %>%
  drop_na(body_mass_g, sex) %>%
  wilcox_test(body_mass_g ~ sex,
              paired = FALSE)

# A tibble: 1 × 7
  .y.         group1 group2    n1    n2 statistic        p
* <chr>       <chr>  <chr>  <int> <int>     <dbl>    <dbl>
1 body_mass_g female male     165   168     6874. 1.81e-15

This is not surprising, that there is a significant difference in body weight between male and female penguins. We can see this clearly in our plot.

How can we add the stats to our plot?

Plot

Using `stat_compare_means()`

The function stat_compare_means() allows mean comparison p-values to be easily added to a ggplot.

Note, the function should look at your data and test for normality and pick the statistical test accordingly. You can see that is working in the chunk below, but I would recommend that you always do your own statistical test and make sure you plot accordingly.

penguins_by_sex +
  stat_compare_means()

penguins_by_sex +
  stat_compare_means(method = "wilcox.test")

Manually with `geom_text()` or `annotate()`

In general, plotting using geom_text() is easier, and follows classic geom_() syntax (e.g., includes aes()) but for some reason these don’t pass as vectorized objects so sometimes it yields low quality images. Using annotate() passes as vectors and thus tends to be higher quality. You can decide which you want to use depending on your purpose.

If I’m being honest, the most common way that I would add statistics to a plot if I was trying to do just a few simple plots at once, would be with annotate() . I like to use annotate() over geom_text() or geom_label() because it is vectorized and don’t become low quality down the road.

With geom_text()

penguins_by_sex +
  geom_text(aes(x = 2, y = 6500, label = "*"), # x, y, and label within aes()
            color = "black", size = 6)

With annotate()

penguins_by_sex +
  annotate(geom = "text", # note no aes()
           x = 2, y = 6500, 
           label = "*", 
           size = 6)

You can also add multiple annotation layers. I’m introducing a new function here, glue() which is amazing for easy syntax pasting of strings with data.

The syntax for glue() is like this:

x <- 2 + 3

glue("2 + 3 = {x}")

2 + 3 = 5

# we did this already, just assigning to object
by_sex_pval <- penguins %>%
  drop_na(body_mass_g, sex) %>%
  wilcox_test(body_mass_g ~ sex,
              paired = FALSE)

# plot
penguins_by_sex +
  ylim(2500, 7500) + # adjust the y-axis so there's space for the label
  annotate(geom = "text", x = 2, y = 6500, label = "*", size = 6) +
  annotate(geom = "text", x = 2, y = 7000,
           label = glue("Wilcoxon signed rank test \np-value = {by_sex_pval$p}"))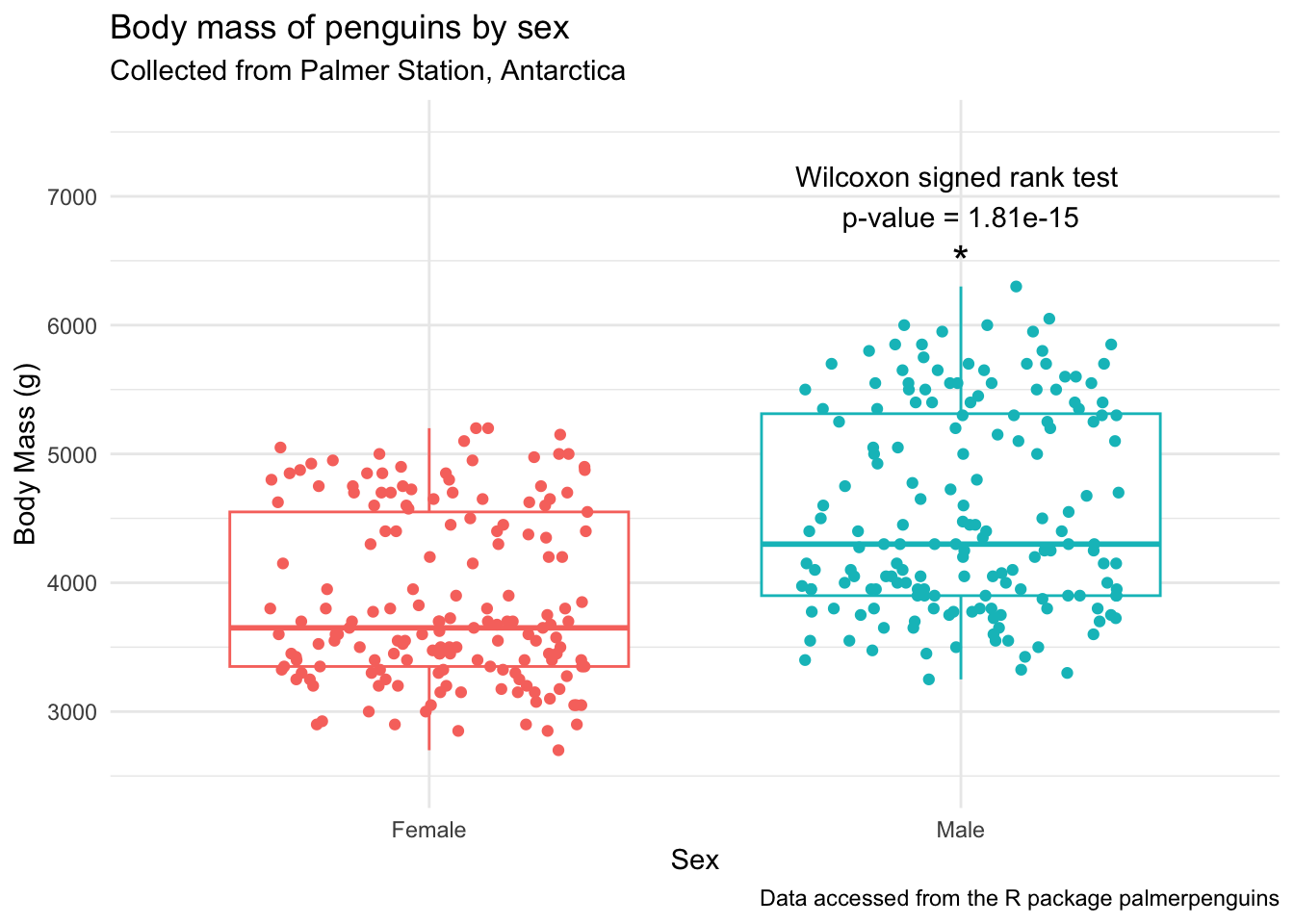

>2 group comparisons (ANOVA or similar)

When we are comparing means between more than 2 samples, we will have to first run a statistical test to see if there are any significant differences among our groups, and then if there are, run a post-hoc test. Before we do that, let’s plot.

Are there significant differences in body mass

(penguins_f_massbyspecies <- penguins %>%
  drop_na(body_mass_g, species, sex) %>%
  filter(sex == "female") %>%
  ggplot(aes(x = species, y = body_mass_g, fill = species)) +
  geom_violin(outlier.shape = NA,
              draw_quantiles = 0.5) + # add the median by drawing 50% quantile
  ggdist::geom_dots(side = "both", color = "black", alpha = 0.8) +
  theme_minimal() +
  theme(legend.position = "none") +
  labs(x = "Penguin Species",
       y = "Body Mass (g)",
       title = "Body mass of female penguins by species",
       subtitle = "Collected from Palmer Station, Antarctica",
       caption = "Data accessed from the R package palmerpenguins"))

Warning in geom_violin(outlier.shape = NA, draw_quantiles = 0.5): Ignoring
unknown parameters: `outlier.shape`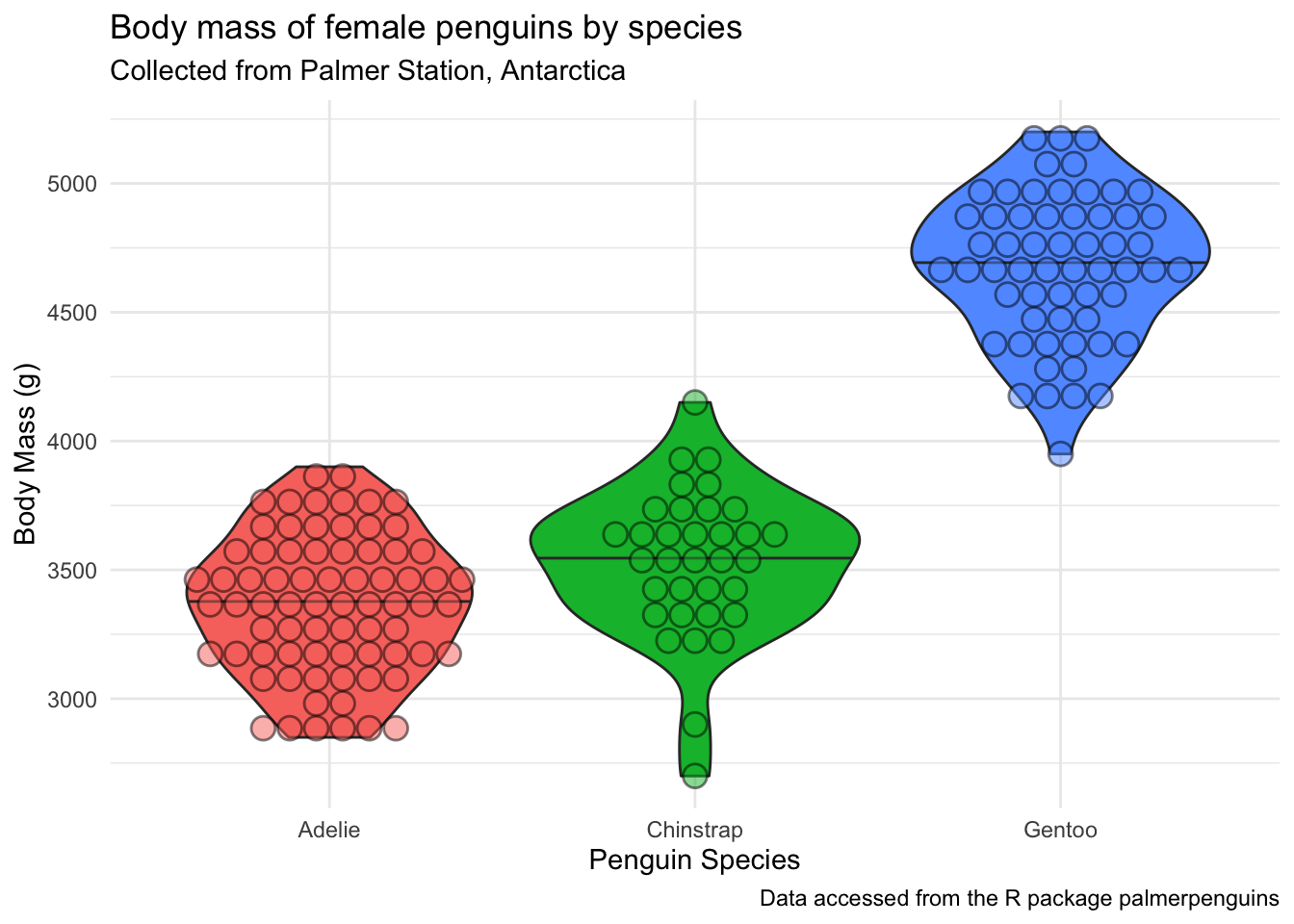

Testing assumptions

Normality

# testing normality by group
penguins %>%
  drop_na(body_mass_g, sex) %>% # remove NAs
  filter(sex == "female") %>%
  group_by(species) %>% # test by species
  shapiro_test(body_mass_g) # test for normality

# A tibble: 3 × 4
  species   variable    statistic     p
  <fct>     <chr>           <dbl> <dbl>
1 Adelie    body_mass_g     0.977 0.199
2 Chinstrap body_mass_g     0.963 0.306
3 Gentoo    body_mass_g     0.981 0.511

# testing normality across all data
penguins %>%
  drop_na(body_mass_g, sex) %>% # remove NAs
  filter(sex == "female") %>%
  shapiro_test(body_mass_g) # test for normality

# A tibble: 1 × 3
  variable    statistic            p
  <chr>           <dbl>        <dbl>
1 body_mass_g     0.919 0.0000000616

Ok looks like we have normally distributed data among the different species of female penguins.

Constant variance

levene_test() which is part of the rstatix package. Again, this is a pipe-friendly wrapper for the function levene.test().

penguins %>%
  drop_na(body_mass_g, sex, species) %>% # remove NAs
  filter(sex == "female") %>%
  levene_test(body_mass_g ~ species) # test for constant variance

# A tibble: 1 × 4
    df1   df2 statistic     p
  <int> <int>     <dbl> <dbl>
1     2   162    0.0357 0.965

We have constant variance. Along with normally distributed data, this means that we can use parametric tests. In the case of >2 samples, that would be ANOVA.

ANOVA

The most commonly used function to run ANOVA in R is called aov() which is a part of the stats package that is pre-loaded with base R. So no new packages need to be installed here.

If we want to learn more about the function aov() we can do so using the code below. The help documentation will show up in the bottom right quadrant of your RStudio.

?aov()

We can run an ANOVA by indicating our model, and here I’m also selecting to drop the NAs for our variables of interest, and filtering within the data = argument.

aov_female_massbyspecies <- 
  aov(data = penguins %>% 
             filter(sex == "female") %>%
             drop_na(body_mass_g, species),
      body_mass_g ~ species)

Now lets look at the aov object.

summary(aov_female_massbyspecies)

             Df   Sum Sq  Mean Sq F value Pr(>F)    
species       2 60350016 30175008   393.2 <2e-16 ***
Residuals   162 12430757    76733                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We can take the output of our ANOVA and use the function tidy() within the broom package to turn our output into a tidy table. Here, the notation broom::tidy() means I want to use the function tidy() that is a part of the broom package. This works even though I haven’t called library(broom) at the beginning of my script.

tidy_anova <- broom::tidy(aov_female_massbyspecies)

knitr::kable(tidy_anova)

term	df	sumsq	meansq	statistic	p.value
species	2	60350016	30175008.01	393.2465	0
Residuals	162	12430757	76733.07	NA	NA

See how this is different from just saving the ANOVA summary? Open both anova_summary and tidy_anova and note the differences.

anova_summary <- summary(aov_female_massbyspecies)

Posthoc group analysis

Now that we see we have a significant difference somewhere in the body mass of the 3 species of female penguins, we can do a posthoc test to see which groups are significantly different. We will do our post-hoc analysis using Tukey’s Honestly Significant Difference test and the function HSD.test() which is a part of the useful package agricolae.

tukey_massbyspecies <- HSD.test(aov_female_massbyspecies, 
                      trt = "species", 
                      console = TRUE) # prints the results to console


Study: aov_female_massbyspecies ~ "species"

HSD Test for body_mass_g 

Mean Square Error:  76733.07 

species,  means

          body_mass_g      std  r  Min  Max
Adelie       3368.836 269.3801 73 2850 3900
Chinstrap    3527.206 285.3339 34 2700 4150
Gentoo       4679.741 281.5783 58 3950 5200

Alpha: 0.05 ; DF Error: 162 
Critical Value of Studentized Range: 3.345258 

Groups according to probability of means differences and alpha level( 0.05 )

Treatments with the same letter are not significantly different.

          body_mass_g groups
Gentoo       4679.741      a
Chinstrap    3527.206      b
Adelie       3368.836      c

Like we did with the aov object, you can also look at the resulting HSD.test object (here, tukey_massbyspecies) in your environment pane.

Here, instead of using the broom package, you can convert the part of the tukey_bill_length object that contains the post-hoc groupings into a dataframe using as.data.frame().

tidy_tukey <- as.data.frame(tukey_massbyspecies$groups)

tidy_tukey

          body_mass_g groups
Gentoo       4679.741      a
Chinstrap    3527.206      b
Adelie       3368.836      c

Plot

Using `stat_compare_means()`

penguins_f_massbyspecies +
  stat_compare_means()

penguins_f_massbyspecies +
  stat_compare_means(method = "anova")

Manually with `geom_text()` or `annotate()`

We want to add the letters to this plot, so we can tell which groups of penguin species are significantly different.

Before we can do this, we will need to do some of everyone’s favorite task, wrangling. We are going to figure out what the maximum body_mass_g for each species is, so it will help us determine where to put our letter labels. Then, we can add our labels to be higher than the largest data point. We will calculate this for each group, so that the letters are always right about our boxplot.

body_mass_max <- penguins %>%
  filter(sex == "female") %>%
  drop_na(body_mass_g, species) %>%
  group_by(species) %>%
  summarize(max_body_mass = max(body_mass_g))

body_mass_max

# A tibble: 3 × 2
  species   max_body_mass
  <fct>             <int>
1 Adelie             3900
2 Chinstrap          4150
3 Gentoo             5200

Let’s add our post-hoc group info to body_mass_max, since those two dataframes are not in the same order. Instead of binding the two dataframes together, we are going to join them using one of the dplyr _join() functions, which allows you to combine dataframes based on a specific common column. The join functions work like this:

inner_join(): includes all rows in x and y.
left_join(): includes all rows in x.
right_join(): includes all rows in y.
full_join(): includes all rows in x or y.

In this case, it doesn’t matter which _join() we use because our dfs all have the exact same rows.

tidier_tukey <- tidy_tukey %>%
  rownames_to_column() %>% # converts rownames to columns
  rename(species = rowname) # renames the column now called rowname to species
  
# join
body_mass_for_plotting <- full_join(tidier_tukey, body_mass_max,
                               by = "species")

Let’s plot. First using geom_text()

penguins_f_massbyspecies +
  geom_text(data = body_mass_for_plotting,
            aes(x = species,
                y = 175 + max_body_mass, 
                label = groups))

Next using annotate().

penguins_f_massbyspecies +
  annotate(geom = "text",
           x = c(3,2,1),
           y = 175 + body_mass_for_plotting$max_body_mass,
           label = body_mass_for_plotting$groups)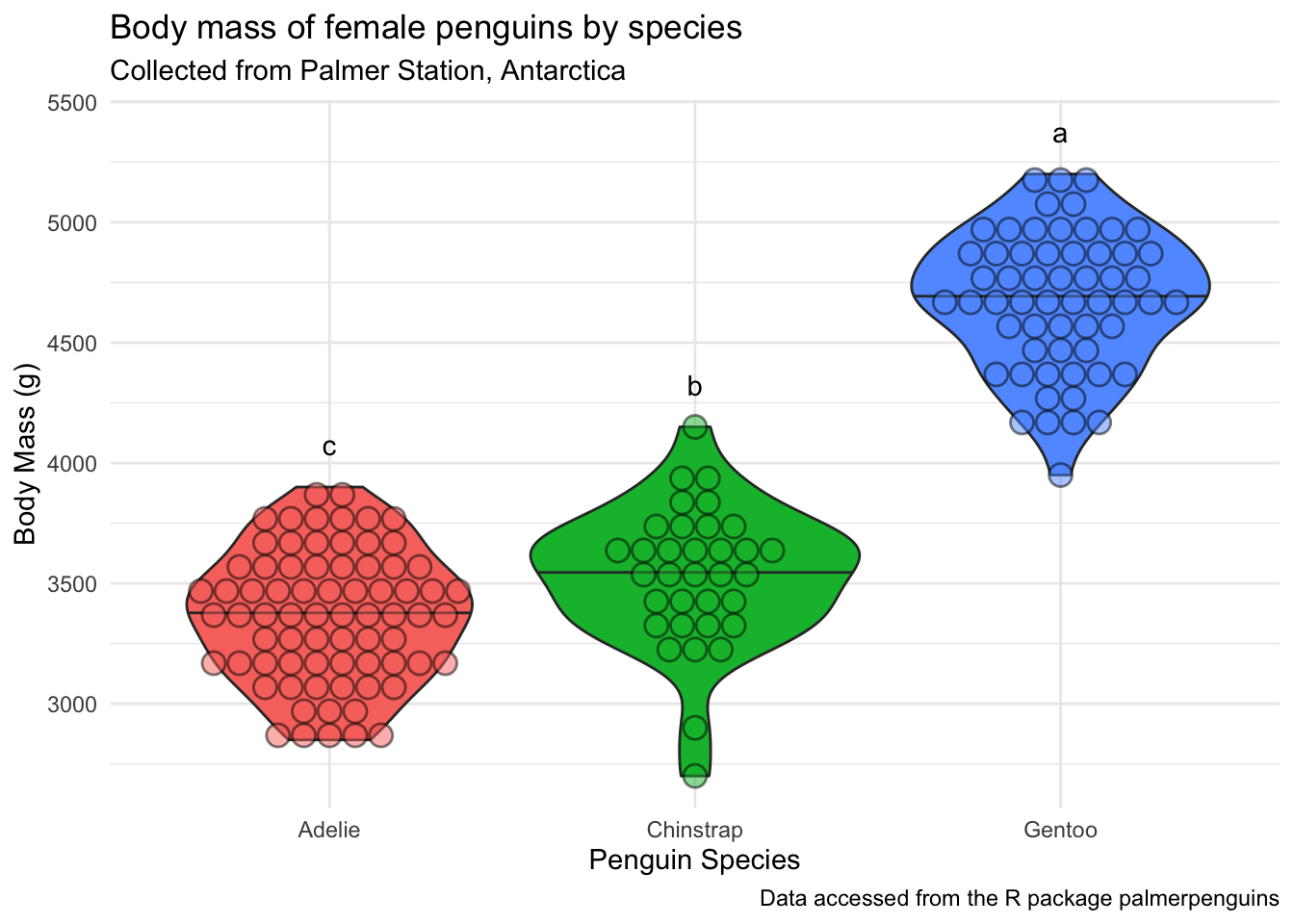

Useful resources

There have been previous Code Club sessions about adding statistics to plots:

Introduction

Load libraries and data

2 group comparisons (t-tests or similar)

Testing assumptions

Normality

Constant variance

Non-parametric t-test

Plot

Using stat_compare_means()

Manually with geom_text() or annotate()

>2 group comparisons (ANOVA or similar)

Testing assumptions

Normality

Constant variance

ANOVA

Posthoc group analysis

Plot

Using stat_compare_means()

Manually with geom_text() or annotate()

Useful resources

Using `stat_compare_means()`

Manually with `geom_text()` or `annotate()`

Using `stat_compare_means()`

Manually with `geom_text()` or `annotate()`